Digraph With Adjacency List

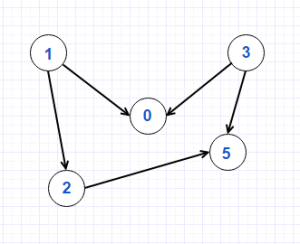
Inspired by Digraph (Algorithms 4/e) – Algorithms, 4th Edition

Digraph.java

//Digraph implementation with adjacency list
public class Digraph<V>{

    private Map<V,List<DirectedEdge<V>>> vertexes;

    private int eCount;

    public Digraph(){
        this.vertexes = new HashMap<>();
    }

    public int V(){
        return vertexes.size();
    }

    public int E(){
        return eCount;
    }

    public List<DirectedEdge<V>> adj(V vertex){
        return vertexes.get(vertex);
    }

    public void addEdge(DirectedEdge<V> de){
        if (de == null){
            return;
        }
        if (!vertexes.containsKey(de.from())){
            vertexes.put(de.from(), new ArrayList<>());
        }
        if (!vertexes.containsKey(de.to())){
            vertexes.put(de.to(), new ArrayList<>());
        }
        vertexes.get(de.from()).add(de);
        ++eCount;
    }

    //O(V+E)
    public List<DirectedEdge<V>> getEdges(){
        List<DirectedEdge<V>> res = new ArrayList<DirectedEdge<V>>(eCount);
        for (V v : vertexes.keySet()){
            res.addAll(vertexes.get(v));
        }
        return res;
    }

    public Set<V> getVertexes(){
        return vertexes.keySet();
    }
}

DirectedEdge.java

public class DirectedEdge<V>{

    private V from;
    private V to;

    public DirectedEdge(V from, V to){
        this.from = from;
        this.to = to;
    }

    public V from(){
        return from;
    }

    public V to(){
        return to;
    }

    @Override
    public String toString(){
        return from.toString() + "-->" + to.toString();
    }

}

Lintcode. Best Time to Buy and Sell Stock I, II, III

Best Time to Buy and Sell Stock I

Say you have an array for which the i^th element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (ie, buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Example
Given array [3,2,3,1,2], return 1.

Python
Time complexity: O(N)
Space complexity: O(1)

class Solution:
    """
    @param prices: Given an integer array
    @return: Maximum profit
    """
    def maxProfit(self, prices):
        # write your code here
        if (not prices or len(prices) <= 1):
            return 0
            
        minSoFar = prices[0]
        profit = 0
        
        for v in prices[1:]:
            minSoFar = min(minSoFar, v)
            profit = max(profit, v - minSoFar)

        return profit

 

Best Time to Buy and Sell Stock II

Say you have an array for which the i^th element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times). However, you may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).

Example
Given an example [2,1,2,0,1], return 2.

Java
Time complexity: O(N)
Space complexity: O(1)

class Solution {
    /**
     * @param prices: Given an integer array
     * @return: Maximum profit
     * As a solution one can find sum of contiguous delta trades, where 
     * 'delta trade' stands for buy-sell compound transaction.
     */
    public int maxProfit(int[] prices) {
        // write your code here
        if (prices == null || prices.length <= 0){
            return 0;
        }
        
        int profit = 0;
        
        for (int i = 1; i < prices.length; ++i){
            profit += Math.max(0, prices[i] - prices[i-1]);
        }
        
        return profit;
    }
}

 

Best Time to Buy and Sell Stock III

Say you have an array for which the i^th element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete at most two transactions.

Notice : You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).

Example

Given an example [4,4,6,1,1,4,2,5], return 6.

Java
Time complexity: O(N)
Space complexity: O(1)

class Solution {
    /**
     * @param prices: Given an integer array
     * @return: Maximum profit
     */
    public int maxProfit(int[] prices) {
        // write your code here
        if (prices == null || prices.length == 0){
            return 0;
        }
        
        int buyFirst = Integer.MIN_VALUE;
        int sellFirst = 0;
        int buySecond = Integer.MIN_VALUE;
        int sellSecond = 0;
        
        for (int i = 0; i < prices.length; ++i){
            buyFirst = Math.max(buyFirst, -prices[i]);
            sellFirst = Math.max(buyFirst + prices[i], sellFirst);
            buySecond = Math.max(buySecond, sellFirst - prices[i]);
            sellSecond = Math.max(sellSecond, buySecond + prices[i]);
        }
        
        return sellSecond;
    }
}

Check If Graph is Bipartite

A Bipartite Graph is a graph whose vertices can be divided into two independent sets, U and V such that every edge (u, v) either connects a vertex from U to V or a vertex from V to U. In other words, for every edge (u, v), either u belongs to U and v to V, or u belongs to V and v to U. We can also say that there is no edge that connects vertices of same set.
A bipartite graph is possible if the graph coloring is possible using two colors such that vertices in a set are colored with the same color.

Below code implements this algorithm.

Java
Time complexity: O(V+E)
Space complexity: O(V)

public class BipartiteGraphValidator {

    public static <V> boolean isBipartite(Graph<V> g){
        if (g == null || g.V() <= 1){
            return false;
        }

        Map<V, Boolean> coloredPath = new HashMap<>();//strongly connected graphs only
        Queue<V> q = new LinkedList<V>();

        V source = g.getVertexes().iterator().next();
        q.offer(source);
        coloredPath.put(source, Boolean.TRUE);

        while (q.size() > 0){
            V curr = q.poll();
            for (V neighb : g.adj(curr)){
                if (coloredPath.containsKey(neighb) && color(curr, coloredPath) == color(neighb, coloredPath)){
                    return false;
                }

                if (!coloredPath.containsKey(neighb)){
                    q.offer(neighb);
                }
                coloredPath.put(neighb, !color(curr, coloredPath));
            }
        }

        return true;
    }

    private static <V> boolean color(V v, Map<V, Boolean> coloredPath){
        return coloredPath.get(v);
    }
}

Trie

Trie, or prefix tree, is a search tree that stores associative arrays or dynamically resizable collections per node. From every regular node one can search a value by key (key defines position of node with corresponding value in collection). Nodes on every path starting from level 0 (direct children of root) share the common prefix. Path from level 0 to terminal node represents a complete word (for example, ‘MAP’).

One can search a word in trie in O(M) time, where M is length of word to be searched. In case of word miss, search will terminate on some node along the path and return faster than in O(M) (depends on concrete structure of trie). Insertions and deletions will perform at worst in O(M).

Java

Time complexity: O(M) for search, insert and delete, M – length of word

Space complexity: O(N*26) -> O(N), per every node we store constant number of references to child nodes, bounded by size of alphabet

class TrieNode {

        public static final int R = 26;//size of alphabet

        private TrieNode[] next = new TrieNode[R];

        private boolean isTerminal;

        // Initialize your data structure here.
        public TrieNode() {

        }
        public void setTerminal(){
            this.isTerminal = true;
        }

        public boolean isTerminal(){
            return isTerminal;
        }

        public TrieNode setNext(int c){
            int k = c - 'a';
            if (next[k] != null){
                return next[k];
            } else {
                TrieNode newNode = new TrieNode();
                next[k] = newNode;
                return newNode;
            }
        }

        public TrieNode getNext(char c){            
            return next[c - 'a'];
        }
}

public class Trie {
        private TrieNode root;

    public Trie() {
        root = new TrieNode();
    }

    // Inserts a word into the trie.
    public void insert(String word) {
        TrieNode curr = root;
        for (Character c : word.toCharArray()){
            curr = curr.setNext(c);
        }
        curr.setTerminal();
    }

    // Returns if the word is in the trie.
    public boolean search(String word) {
        TrieNode curr = root;
        for (Character c : word.toCharArray()){
            curr = curr.getNext(c);
            if (curr == null){
                return false;
            }
        }
        return curr.isTerminal();
    }

    // Returns if there is any word in the trie
    // that starts with the given prefix.
    public boolean startsWith(String prefix) {
        TrieNode curr = root;
        for (Character c : prefix.toCharArray()){
            curr = curr.getNext(c);
            if (curr == null){
                return false;
            }
        }
        return true;
    }
}

Lintcode. Topological Sort

Given an directed graph, a topological order of the graph nodes is defined as follow:

• For each directed edge A -> B in graph, A must be before B in the order list.
• The first node in the order can be any node in the graph with no nodes direct to it.

Find any topological order for the given graph. You can assume that there is at least one topological order in the graph and graph is of DAG type (directed acyclic graph).

Example

For given graph

The topological order can be:

1, 3, 0, 2, 5
3, 1, 2, 5, 0

Topological sort is commonly used for dependencies resolution in processes like instruction scheduling or defining build order of compilation units. For more information, please watch Topological Sort by Prof. Sedgewick

Java (reverse DFS)
Time complexity: O(V + E), V – num of vertexes, E – num of edges
Space complexity: O(V) + O(E) (for recursive call stack), V – num of vertexes, E – num of edges

/**
 * Definition for Directed graph.
 * class DirectedGraphNode {
 *     int label;
 *     ArrayList<DirectedGraphNode> neighbors;
 *     DirectedGraphNode(int x) { label = x; neighbors = new ArrayList<DirectedGraphNode>(); }
 * };
 */
public class Solution {
    /**
     * @param graph: A list of Directed graph node
     * @return: Any topological order for the given graph.
     */    
    public ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
        // write your code here
        if (graph == null || graph.isEmpty()){
            return new ArrayList<>();
        }
        
        Stack<DirectedGraphNode> stack = new Stack<>();
        Set<Integer> seen = new HashSet<>();
        
        for (DirectedGraphNode node : graph){
            reverseDFS(node, seen, stack);     
        }
        
        Collections.reverse(stack);
        
        return new ArrayList<>(stack);
        
    }
    
    private void reverseDFS(DirectedGraphNode node, Set<Integer> seen, Stack<DirectedGraphNode> stack){
        if (seen.contains(node.label)){
            return;
        }
        
        for (DirectedGraphNode neighbour : node.neighbors){
            if (!seen.contains(neighbour.label)){
                reverseDFS(neighbour, seen, stack);    
            }
        }
        
        stack.push(node);
        seen.add(node.label);
    }
}

Java (BFS)
Time complexity: O(V*D)(to init degree map) + O(V + E), V – num of vertexes, D – max vertex degree, E – num of edges
Space complexity: O(V), V – num of vertexes

/**
 * Definition for Directed graph.
 * class DirectedGraphNode {
 *     int label;
 *     ArrayList<DirectedGraphNode> neighbors;
 *     DirectedGraphNode(int x) { label = x; neighbors = new ArrayList<DirectedGraphNode>(); }
 * };
 */
public class Solution {
    /**
     * @param graph: A list of Directed graph node
     * @return: Any topological order for the given graph.
     */    
    public ArrayList<DirectedGraphNode> topSort(ArrayList<DirectedGraphNode> graph) {
        // write your code here
        if (graph == null || graph.size() == 0){
            return new ArrayList<>();
        }
        
        Map<DirectedGraphNode, Integer> inDegreeMap = getInDegreeMap(graph);
        Queue<DirectedGraphNode> q = new LinkedList<>();
        
        for (DirectedGraphNode node : graph){
            if (!inDegreeMap.containsKey(node)){
                q.offer(node);
            }
        }
        
        if (q.isEmpty()){//graph has cycles, not possible to build topSort
            return new ArrayList<>();    
        }
        
        ArrayList<DirectedGraphNode> res = new ArrayList<>();
        
        while (!q.isEmpty()){
            DirectedGraphNode curr = q.poll();
            res.add(curr);
            for (DirectedGraphNode neighb : curr.neighbors){
                int inDegree = inDegreeMap.get(neighb);
                inDegreeMap.put(neighb, inDegree - 1);
                if (inDegree - 1 == 0){
                    q.offer(neighb);
                }
            }
        }
        
        return res;
        
        
    }
    
    private Map<DirectedGraphNode, Integer> getInDegreeMap(List<DirectedGraphNode> graph){
        Map<DirectedGraphNode, Integer> inDegreeMap = new HashMap<>();  
        for (DirectedGraphNode node : graph){
            for (DirectedGraphNode neighb : node.neighbors){
                if (!inDegreeMap.containsKey(neighb)){
                    inDegreeMap.put(neighb, 1);
                } else {
                    inDegreeMap.put(neighb, inDegreeMap.get(neighb) + 1);
                }
            }
        }
        
        return inDegreeMap;
    }
    
}

Subset Sum

Given a set of non-negative integers, and a value sum, determine if there is a subset of the given set with sum equal to given sum.

Examples: set[] = {3, 34, 4, 12, 5, 2}, sum = 9
Output:  True  //There is a subset (4, 5) with sum 9.

Java (bottom-up)
Time complexity: O(N*M), N – size of array, M – target sum
Space complexity: O(N*M), N – size of array, M – target sum

public class SubSetSum {

    public boolean sumsTo(int[] nums, int sum){
        if (nums == null || nums.length == 0 || sum < 0){
            return false;
        }

        boolean[][] dp = new boolean[nums.length][sum+1];

        for (int i = 0; i < nums.length; ++i){
            dp[i][0] = true;
        }

        for (int i = 0; i < dp.length; ++i){
            for (int j = 1; j < dp[0].length; ++j){
                if (i == 0 && nums[i] == j){
                    dp[i][j] = true;
                } else if (i == 0){
                    continue;
                }else {
                    dp[i][j] = dp[i-1][j] || (nums[i] <= j ? dp[i-1][j - nums[i]] : false);
                }

            }
        }

        return dp[nums.length - 1][sum];
    }

}

Python (top-down)
Time complexity: O(2^N), N – size of array
Space complexity: O(N), N – size of array

def sumsTo(nums, sum):
    if not len(nums) or sum < 0:
        return False

    dp = [None] * len(nums)
    return checkSumsTo(nums, 0, sum, dp)

def checkSumsTo(nums, idx, sum, dp):
    if sum == 0:
        return True
    elif sum < 0 or idx >= len(nums):
        return False
    elif idx < len(nums) and dp[idx]:
        return dp[idx]

    notInclude = checkSumsTo(nums, idx+1, sum, dp)
    include = checkSumsTo(nums, idx+1, sum - nums[idx], dp)
    dp[idx] = notInclude or include

    return dp[idx]

Leetcode. Single Number I, II, III

Single Number I

Given an array of integers, every element appears twice except for one. Find that single one.

Note:
Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

Python (v1)
Time complexity: O(N)
Space complexity: O(1)

class Solution(object):
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        xor = 0
        for n in nums:
            xor ^= n
        return xor

Python (v2)
Time complexity: O(N)
Space complexity: O(1)

from functools import reduce
class Solution(object):
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        xor = reduce((lambda x, y: x ^ y), nums)
        return xor

 

Single Number II

Given an array of integers, every element appears three times except for one. Find that single one.

Note:
Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

Java (extra memory)
Time complexity: O(N)
Space complexity: O(1)

public class Solution {
    public int singleNumber(int[] A) {
        // write your code here
        if (A.length == 1){
            return A[0];
        }
        
        int[] bitCount = new int[32];
        for (int a : A){
            for (int i = 0; i < 32; ++i){
                boolean isSet = (a & (1 << i)) != 0; if (isSet){ bitCount[i] = (bitCount[i] + 1) % 3; } } } int res = 0; for (int i = 31; i >= 0; --i){
            res |= bitCount[i] << i;    
        }
        
        return res;
            
    }
}

Java
Time complexity: O(N)
Space complexity: O(1)

public class Solution {
    public int singleNumber(int[] A) {
        // write your code here
        int ones = 0;
        int twos = 0;
        for (int i = 0; i < nums.length; ++i){
            ones = (ones ^ nums[i]) & ~twos;
            twos = (twos ^ nums[i]) & ~ones;
        }
        return ones;            
    }
}

Java (extended to 4 times case)
Time complexity: O(N)
Space complexity: O(1)

public class Solution {
    public int singleNumber(int[] A) {
        int ones = 0;
        int twos = 0;

        for (int i = 0; i < nums.length; ++i){
            ones = (ones ^ nums[i]) & ~(twos & ones);
            twos = (twos ^ nums[i]) & ~ones & ~(twos & ones);
        }
        return ones;           
    }
}

 

Single Number III

Given an array of numbers nums, in which exactly two elements appear only once and all the other elements appear exactly twice. Find the two elements that appear only once.

For example:

Given nums = [1, 2, 1, 3, 2, 5], return [3, 5].

Note:

1. The order of the result is not important. So in the above example, [5, 3] is also correct.
2. Your algorithm should run in linear runtime complexity. Could you implement it using only constant space complexity?

Java
Time complexity: O(N)
Space complexity: O(1)

public class Solution {
    public int[] singleNumber(int[] nums) {
        // write your code here
        int[] res = new int[2];
        
        if (nums == null || nums.length == 0){
            return res;
        }
        
        int diff = 0;
        
        for (int n : nums){
            diff ^= n;
        }
        
        diff &= ~(diff - 1);
        
        for (int n : nums){
            if ((n & diff) != 0){
                res[0] ^= n;
            } else {
                res[1] ^= n;    
            } 
        }
        
        return res;
           
    }
}

Lintcode. Best Time to Buy and Sell Stock IV

 
Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete at most k transactions.

You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

Example

Given prices = [4,4,6,1,1,4,2,5], and k = 2, return 6.

Java
Time complexity: O(K*N^2), N – number of days, k – number of transactions
Space complexity: O(N*K), N – number of days, k – number of transactions

class Solution {
    /**
     * @param k: An integer
     * @param prices: Given an integer array
     * @return: Maximum profit
     */
    public int maxProfit(int k, int[] prices) {
        // write your code here
        if (prices == null || prices.length == 0){
            return 0;
        }
        
        if (k >= prices.length) {
    		int profit = 0;
    		for (int i = 1; i < prices.length; i++) { if (prices[i] > prices[i - 1]) {
    				profit += prices[i] - prices[i - 1];
    			}
    		}
    		return profit;
    	}
        
        int[][] dp = new int[k+1][prices.length];
        
        for (int i = 1; i < dp.length; ++i){
            int profit = 0;
            for (int j = 1; j < dp[0].length; ++j){
                for (int m = 0; m < j; ++m){
                    profit = Math.max(profit, prices[j] - prices[m] + dp[i-1][m]);
                }
                dp[i][j] = Math.max(dp[i][j-1], profit);       
            } 
            
        }
        
        return dp[k][prices.length - 1];
    }
}

Java (optimized)
Time complexity: O(K*N), N – number of days, k – number of transactions
Space complexity: O(N*K), N – number of days, k – number of transactions

class Solution {
    /**
     * @param k: An integer
     * @param prices: Given an integer array
     * @return: Maximum profit
     */
    public int maxProfit(int k, int[] prices) {
        // write your code here
        if (prices == null || prices.length == 0){
            return 0;
        }
        
        if (k >= prices.length) {
    		int profit = 0;
    		for (int i = 1; i < prices.length; i++) {
    			if (prices[i] > prices[i - 1]) {
    				profit += prices[i] - prices[i - 1];
    			}
    		}
    		return profit;
    	}
        
        int[][] dp = new int[k+1][prices.length];
        
        for (int i = 1; i < dp.length; ++i){
            int profit = 0;
            int maxDiff = -prices[0];
            for (int j = 1; j < dp[0].length; ++j){
                dp[i][j] = Math.max(dp[i][j-1], prices[j] + maxDiff); 
                maxDiff = Math.max(maxDiff, dp[i-1][j] - prices[j]);
            } 
            
        }
        
        return dp[k][prices.length - 1];
    }
}

Lintcode. Spiral Matrix

Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.

Example

Given the following matrix:

[

 [ 1, 2, 3 ],

 [ 4, 5, 6 ],

 [ 7, 8, 9 ]

]

You should return [1,2,3,6,9,8,7,4,5].

 

Java
Time complexity: O(N*M), N – num of rows, M – num of columns
Space complexity: O(N*M), N – num of rows, M – num of columns

public class Solution {
    /**
     * @param matrix a matrix of m x n elements
     * @return an integer list
     */
    public List<Integer> spiralOrder(int[][] matrix) {
        // Write your code here
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0){
            return new ArrayList<>();
        }
        
        int nRow = matrix.length;
        int nCol = matrix[0].length;
        
        List<Integer> res = new ArrayList<>();
        int lvlNum = Math.min(nRow, nCol) / 2 + (Math.min(nRow,nCol) % 2 > 0 ? 1 : 0);

        
        for (int level = 0; level < lvlNum; ++level){
            for (int col = level; col < nCol - level; ++col){
                res.add(matrix[level][col]);
            }
            for (int row = level + 1; row < nRow - level; ++row){
                res.add(matrix[row][nCol-level-1]);
            }
            if (nRow-level-1 == level){//avoid row overlap
                break;
            }
            for (int col = nCol - level - 2; col >= level; --col){
                res.add(matrix[nRow-level-1][col]);
            }
            if (level == nCol-level-1){//avoid column overlap
                break;    
            }
            for (int row = nRow-level-2; row > level; --row){
                res.add(matrix[row][level]);
            }
        }
        
        return res;
    }
}

Lintcode. Longest Common Subsequence

Given two strings, find the longest common subsequence (LCS).
Your code should return the length of LCS.

Clarification
What’s the definition of Longest Common Subsequence?

https://en.wikipedia.org/wiki/Longest_common_subsequence_problem

Example
For “ABCD” and “EDCA”, the LCS is “A” (or “D”, “C”), return 1.
For “ABCD” and “EACB”, the LCS is “AC”, return 2.

 

Java (bottom-up)
Time complexity: O(N*M), N – len of string1, M – len of string2
Space complexity: O(N*M), N – len of string1, M – len of string2

public class Solution {
    /**
     * @param A, B: Two strings.
     * @return: The length of longest common subsequence of A and B.
     */
    public int longestCommonSubsequence(String A, String B) {
        // write your code here
        if (A == null || B == null || A.length() == 0 || B.length() == 0){
            return 0;
        }
        
        int[][] dp = new int[A.length()][B.length()];
        
        for (int i = 0; i < A.length(); ++i){
            for (int j = 0; j < B.length(); ++j){
                if (i == 0){
                    dp[i][j] = A.charAt(i) == B.charAt(j) ? 1 : 0;
                } else {
                    int same = A.charAt(i) == B.charAt(j) ? 1 : 0;
                    if (same == 1){
                        dp[i][j] = same + ((i > 0 && j > 0) ? dp[i-1][j-1] : 0);
                    } else{
                        int prevNonSymm1 = j > 0 ? dp[i][j-1] : Integer.MIN_VALUE; 
                        int prevNonSymm2 = i > 0 ? dp[i-1][j] : Integer.MIN_VALUE;
                        dp[i][j] = Math.max(prevNonSymm1, prevNonSymm2);   
                    }
                }
            }    
        }
        return dp[A.length()-1][B.length() - 1];
    }
}

 

Python (bottom-up)

class Solution:
    """
    @param A, B: Two strings.
    @return: The length of longest common subsequence of A and B.
    """
    def longestCommonSubsequence(self, A, B):
        # write your code here
        if (not len(A) or not len(B)):
            return 0
            
        dp = [[0 for x in range(len(A))] for y in range(len(B))] 
        
        for x in range(len(A)):
            for y in range(len(B)):
                if A[x] == B[y]:
                    dp[x][y] = 1 if not x or not y else 1 + dp[x-1][y-1]
                elif (x > 0 and y > 0):
                    dp[x][y] = max(dp[x-1][y], dp[x][y-1])
                else: 
                    dp[x][y] = dp[x-1][y] if x else dp[x][y-1] if y else 0

        return dp[len(A)-1][len(B)-1]

Java (topdown)
Time complexity: O(N*M), N – len of string1, M – len of string2
Space complexity: O(N*M) (dp array) + O(N*M) (recursive stack), N – len of string1, M – len of string2

public class Solution {
    /**
     * @param A, B: Two strings.
     * @return: The length of longest common subsequence of A and B.
     */
    public int longestCommonSubsequence(String A, String B) {
        // write your code here
        if (A == null || B == null || A.length() == 0 || B.length() == 0){
            return 0;
        }
        
        int[][] dp = new int[A.length()][B.length()];
        
        return lcs(A, B, 0, 0, dp);
    }
    
    private int lcs(String A, String B, int idxa, int idxb, int[][] dp){
        if (idxa == A.length() || idxb == B.length()){
            return 0;
        }
        
        if (dp[idxa][idxb] != 0){
            return dp[idxa][idxb];
        }
        
        int lcsLen = 0;
        
        if (A.charAt(idxa) == B.charAt(idxb)){
            lcsLen = 1 + lcs(A, B, idxa+1, idxb+1, dp);    
        } else {
            lcsLen = Math.max(lcs(A, B, idxa+1, idxb, dp), lcs(A, B, idxa, idxb+1, dp)); 
        }
        
        dp[idxa][idxb] = lcsLen;
        
        return lcsLen;
    }
}